1. CS 특강(CPU): 강창민 튜터님
CS 기초지식 확보목적
CPU는 4가지의 기능이 있다
Fetch/ Decode/ Execute/ Writeback
1) 왜 싱글코어가 아닌 멀티 코어를 사용하는지?
2) CPU 구조, 구성원
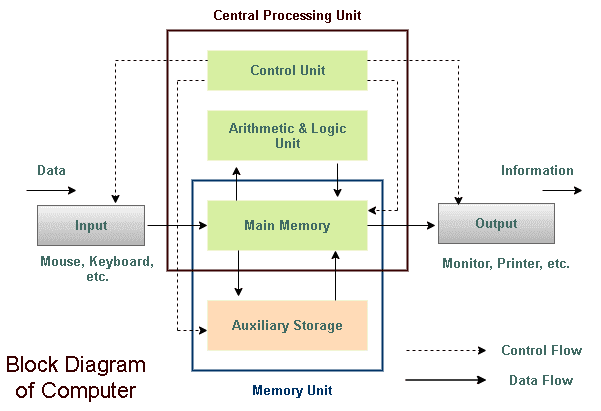
3) CPU와 프로그래머 간 통신 방법
4) 명령어 수행방법
**OS/ DB/ 네트워크 필수학습, 컴파일러/프로그래밍언어 보강
2.알고리즘 강의
트리/힙
트리 : 비선형 구조 ( vs 큐, 스택 )

Node: 트리에서 데이터를 저장하는 기본 요소
Root Node: 트리 맨 위에 있는 노드
Level: 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
Parent Node: 어떤 노드의 상위 레벨에 연결된 노드
Child Node: 어떤 노드의 하위 레벨에 연결된 노드
Leaf Node(Terminal Node): Child Node가 하나도 없는 노드
Sibling: 동일한 Parent Node를 가진 노드
Depth: 트리에서 Node가 가질 수 있는 최대 Level
BInary Tree : 자식 노드가 무조건 두 개(0.1. 2) 이하 + 완전 이진 트리( 왼쪽부터 자식 노드가 채워진)
트리 구현
인덱스에 0을 넣지 않는다. -> 0 대신 None, 편의성을 위해(Why?: )
1. 현재 인덱스 * 2 -> 왼쪽 자식의 인덱스
2. 현재 인덱스 * 2 + 1 -> 오른쪽 자식의 인덱스
3. 현재 인덱스 // 2 -> 부모의 인덱스
완전 이진 트리의 경우,
각 레벨에 최대로 들어갈 수 있는 노드의 개수는 2^k개
높이 h가 주어질 경우, 최대 노드 개수는 2^(h+1)-1
이진 트리의 높이는 최대로 해봤자 O(log(N))
높이에 대한 인덱스를 시간 복잡도로 표현하고 알아야하는 이유 + 힙
힙 ~ 부모보다 잘난 자식이 없어! 최고 힙하다/ 자식이기는 부모 없다더니, 정말 최소로 힙하네
데이터에서 최대값과 최소값을 빠르게 찾기 위한 완전 이진 트리의 한 종류
*Max 힙은 항상 최대값이 가장 위로 올라온다
맥스 힙의 노드 추가
#1. 새 노드를 맨 끝에 추가한다
#2. 새 노드를 부모 노드와 비교한다. 크다면 교체한다
#3. 꼭대기까지 반복한다.
맥스 힙의 노드 제거
#1. 루트 노드와 맨 끝에 있는 노드를 교체한다
#2. 맨 뒤에 있는 노드(원래 루트 노르)를 삭제. 끝에 반환해줘야 하므로 저장합니다
#3. 변경된 노드와 자식 노드들을 비교. 더 큰 노드가 부모 노드 자리로 교체된다.
#4. 자식 노드 둘 보다 부모 노드가 크거나(교체가 일어나지 않거나) 가장 바닥에 도달할 때까지 교체를 반복
#5. 삭제된 노드(2에서 저장한 기존의 루트 노드)를 반환한다*Min 힙은 항상 최소값이 가장 위로 올라온다
'내일배움캠프 4기 스프링 > 내배캠 TIL📘' 카테고리의 다른 글
| 11. 15 JAVA 기초 강의/ 알고리즘 강의 + 그림으로 배우는 알고리즘 (0) | 2022.11.15 |
|---|---|
| 11. 14 알고리즘 강의/ JAVA 기초 강의/ 그림으로 배우는 알고리즘/ Leetcode (0) | 2022.11.14 |
| 11. 10 JAVA 기초 강의/ 알고리즘 강의/ 알고리즘 특강 (2) | 2022.11.10 |
| 11. 09 파이썬 기초 강좌/ 알고리즘 강의/ 알고리즘 특강/ JAVA 정석 + 기초 (0) | 2022.11.09 |
| 11. 08 파이썬 기초 강좌/ JAVA 기초 강좌/ 알고리즘 강좌 + 코테 문풀 (0) | 2022.11.08 |


